Paper Reading on Deep Compressed Sensing

1. Learning a Compressed Sensing Measurement Matrix via Gradient Unrolling

1.1 Abstract

Linear encoding of sparse vectors is widely popular, but is commonly data-independent – missing any possible extra (but a priori unknown) structure beyond sparsity. In this paper, we present a new method to learn linear encoders that adapt to data, while still performing well with the widely used $\mathcal{l}_1$ decoder. The convex $\mathcal{l}_1$ decoder prevents gradient propagation as needed in standard gradient-based training. Our method is based on the insight that unrolling the convex decoder into T projected subgradient steps can address this issue. Our method can be seen as a data-driven way to learn a compressed sensing measurement matrix. We compare the empirical performance of 10 algorithms over 6 sparse datasets (3 synthetic and 3 real). Our experiments show that there is indeed additional structure beyond sparsity in the real datasets; our method is able to discover it and exploit it to create excellent reconstructions with fewer measurements (by a factor of 1.1-3x) compared to the previous state-of-the-art methods. We illustrate an application of our method in learning label embeddings for extreme multi-label classification, and empirically show that our method is able to match or outperform the precision scores of SLEEC, which is one of the state-of-the-art embedding-based approaches.

1.2 Introduction

Design a measurement matrix $A \in \mathbb{R}^{m \times d}$, such that for an ill-posed problem $y = Ax$ where $x \in \mathbb{R}^d$ and $y \in \mathbb{R}^m$, and $m < d$. The problem of designing measurement matrices and reconstruction algorithms that recover sparse vectors from linear observations is called Compressed Sensing (CS), Sparse Approximation or Sparse Recovery Theory.

The problem can be solved as follows:

$\argmin _{x' \in \mathbb{R}^d} \parallel x' \parallel _0 \quad \mathrm{s.t.} \quad Ax'=y$

But it's a NP-Hard problem. With some properties such as Restricted Isometry Property (RIP) or the nullspace condition (NSP), $\mathcal{l}_0$ norm can be relaxed to $\mathcal{l}_1$ norm:

$D(A, y) = \argmin _{x' \in \mathbb{R}^d} \parallel x' \parallel _1 \quad \mathrm{s.t.} \quad Ax'=y$

The authors interested in vectors that are not only sparse but have additional structure in their support. They propose a data-driven algorithm that learns a good linear measurement matrix $A$ from data samples. Their linear measurements are subsequently decoded with the $\mathcal{l}_1$-minimization to estimate the unknown vector x.

Our method is an autoencoder for sparse data, with a linear encoder (the measurement matrix) and a complex non-linear decoder that approximately solves an optimization problem.

PCA is a data-driven dimensionality reduction method and an autoencoder with encoder and decoder all linear, and is provides the lowest MSE. Linear encoder has advantages, 1) easy to compute matrix-vector multiplication; 2) easy to interpret as every column of the encoding matrix can be viewed as feature embedding. Arora et al. found that pre-trained word embeddings such as GloVe and word2vec formed a good measurement matrices for text data, which need fewer mearusements than random matrces when used with $\mathcal{l}_1$-minimization.

Given $n$ sparse samples $x_1, x_2, \dots, x_n \in \mathbb{R}^d$, our problem is to find the best $A$:

$\min \limits_{A \in \mathbb{R}^{m \times d}} f(A), \quad \mathrm{where} \quad f(A) := \sum_{i=1}^{n} \parallel x_i - D(A, Ax_i) \parallel_2^2$

where $D(·,·)$ is the $\mathcal{l}_1$ decoder.

$f(A)$关于$A$的梯度很难求解，因为$D(\cdot, \cdot)$是由一个优化问题确定的。作者的创新点就在这里，将$\mathcal{l}_1$最小化转变成了T步的投影子梯度的更新，这样梯度就可以计算了。即

$\begin{aligned} \hat{f}(A) :&= \sum_{i=1}^n \lVert x_i - \hat{x}_i\rVert^2_2, \mathrm{where} \\ \hat{x}_i &=T\mathrm{step \, subgradient \, of\, } D(A,Ax_i), \mathrm{for}\, i = 1,2,\cdots,n. \end{aligned}$

这个步骤就被称为梯度展开（gradient unrolling）。推导过程：

• 原始最小化问题：

$\min_{x'\in \mathbb{R}^d} \lVert x' \rVert_1 \quad \mathrm{s.t.} \quad Ax'=y$

• 映射子梯度方法的更新为

$x^{(t+1)} = \Pi(x^{(t)} - \alpha_t g^{(t)}), \quad \mathrm{where} \quad g^{(t)} = \mathrm{sign}(x^{(t)})$

其中，$\Pi$表示到凸集$\{x':Ax'=y\}$上的投影，$g^{(t)}$是符号函数，也就是$\lVert\cdot\rVert_1$在$x^{(t)}$处的子梯度，$\alpha_t$是第t个迭代的步长。因为$A$是行满秩矩阵，$\Pi$有如下闭式解：

$\begin{aligned} \Pi(z) & = \argmin_h\lVert h-z\rVert_2^2 \quad \mathrm{s.t.} Ah=y \\ &=z + \argmin_{h'}\lVert h'\rVert_2^2 \quad \mathrm{s.t.} Ah'=y-Az \\ &= z + A^{+}(y-Az) \end{aligned}$

这里的$A^+ = A^\mathrm{T}(AA^\mathrm{T})^{-1}$是$A$的伪逆。带入上式，又$Ax^{(t)}=y$，有

$x^{(t+1)} = x^{(t)} - \alpha_t (I-A^+A)\mathrm{sign}(x^{(t)})$

使用$x^{(1)}=A^+y$作为起始点。

根据一个引理，我们有理由使用$A^\mathrm{T}$来替换$A^+$，因为$A^+$的计算很麻烦，而且难以反向传播。具体的引理内容参见论文。最终的迭代形式成为：

$x^{(t+1)} = x^{(t)} - \alpha_t (I-A^\mathrm{T}A)\mathrm{sign}(x^{(t)})$

引理要求$A$的奇异值都为1，训练时并没有添加这个约束，但是最终得到的测量矩阵和约束集很接近。网络结构如下：

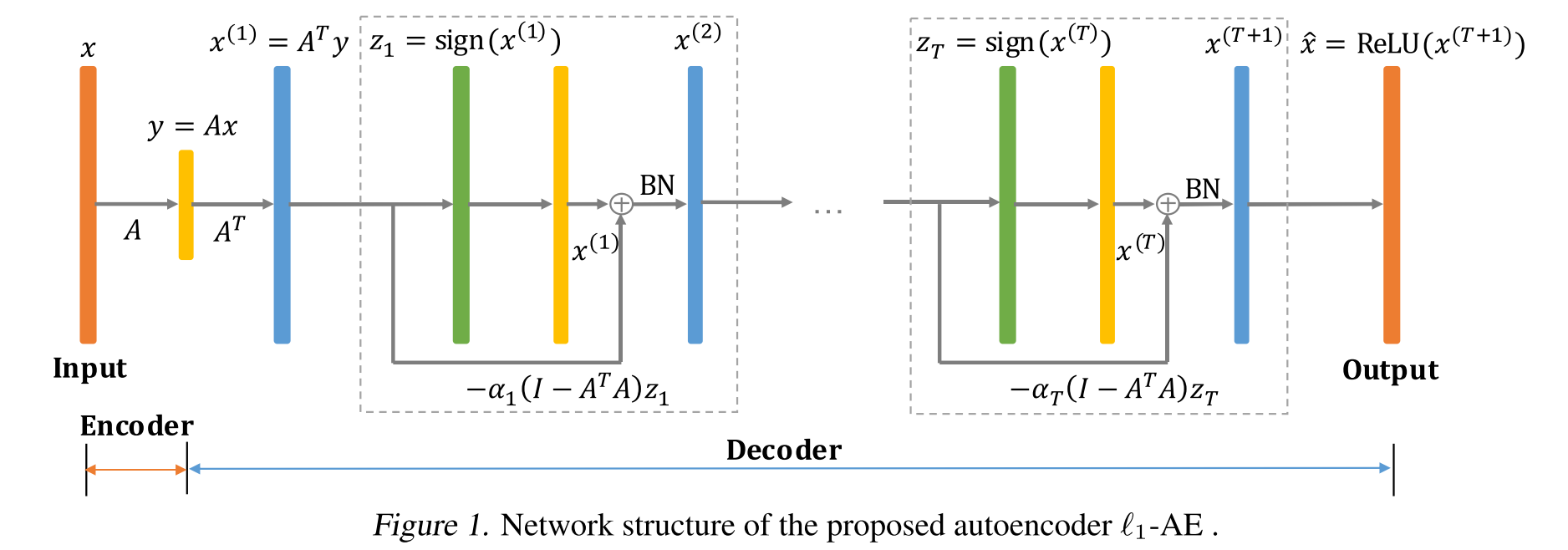
经过$T$个 block，输出为$x^{(T+1)}$，再进入激活层，最终输出为$\hat{x}=\mathrm{ReLU}(x^{(T+1)})$。对于给定的n个无标签训练数据，我们训练的目的是减小$x$与$\hat{x}$之间的均方$\mathcal{l}_2$距离：

$\min_{A\in \mathbb{R}^{m\times d}, \beta\in \mathbb{R}}\frac{1}{n}\sum_{i=1}^n \lVert x-\hat{x}\rVert_2^2$

对于这样学到的线性编码器$A$，我们可以使用$\mathcal{l}_1$解码器进行解码，作者使用Gurobi进行解码，因此整套算法可以写成L1-AE+L1-min pos。这样学到的编码器与$\mathcal{l}_1$解码器和基于模型的解码器都可以有很好的表现。

作者还发现$L1AE$可以用于XML（极多标签学习）。

2. Deep Compressed Sensing

2.1 Abstract

Compressed sensing (CS) provides an elegant framework for recovering sparse signals from compressed measurements. For example, CS can exploit the structure of natural images and recover an image from only a few random measurements. CS is flexible and data efficient, but its application has been restricted by the strong assumption of sparsity and costly reconstruction process. A recent approach that combines CS with neural network generators has removed the constraint of sparsity, but reconstruction remains slow. Here we propose a novel framework that significantly improves both the performance and speed of signal recovery by jointly training a generator and the optimisation process for reconstruction via metalearning. We explore training the measurements with different objectives, and derive a family of models based on minimising measurement errors. We show that Generative Adversarial Nets (GANs) can be viewed as a special case in this family of models. Borrowing insights from the CS perspective, we develop a novel way of improving GANs using gradient information from the discriminator.

压缩传感（CS）提供了一个优雅的框架，可从压缩测量中恢复稀疏信号。例如，CS可以利用自然图像的结构并仅从几个随机测量中恢复图像。CS具有灵活性和数据效率，但是其应用受到稀疏性的强烈假设与昂贵的重建过程的限制。将CS与神经网络生成器结合在一起的最新方法消除了稀疏性的约束，但是重建仍然很慢。在这里，我们提出了一个新颖的框架，该框架通过联合训练生成器和通过元学习进行重构的优化过程，可以显着提高信号恢复的性能和速度。我们探索了训练具有不同目标的测量，并基于最小化测量误差得出一系列模型。我们表明，在该系列模型中，可以将生成对抗网络（GAN）视为特例。从CS角度汲取见解，我们开发了一种使用鉴别器中梯度信息来改进GAN的新颖方法。

2.2 Introduction

编解码是通信的核心问题，压缩感知（CS）提供了一个将编码和解码分离成独立的测量和重建过程的框架。

• 自动编码器：端到端训练
• CS：在线优化，从低维测量中恢复高维信号，很少或不需训练

但是CS在处理大规模数据时却因为稀疏假设与重建效率而被阻碍。Bora et al., 2017将CS与独立训练的神经网络生成器合并。本文则提出深度压缩感知（Deep Compressed Sensing，DCS）框架，神经网络同时对测量和重建从头训练。这个框架自然导出了一系列模型，包括GAN，是通过训练不同目标的测量函数得到。文章的贡献有：

• 展示了如何在CS框架内训练深度神经网络
• 元学习的重建过程导致更精确、数量级上更快的方法
• 开发了基于潜在优化的GAN训练算法，提升了GAN的性能，使用不饱和生成器损失$-\mathrm{ln}(D(G(z))$作为测量误差
• 我们将框架扩展到半监督的GAN，并表明潜在优化在语义上有意义的潜在空间中产生

2.3 Background

2.3.1 Compressed Sensing

参考自Donoho, 2006; Candes et al., 2006。

$\boldsymbol m = \mathbf{F}\boldsymbol x + \eta$

式中$\eta$是高斯噪声，$F$为$C\times D$的测量矩阵，$C\ll D$，这样$m$的维度远低于$x$。当$x$是稀疏，且$F$是随机矩阵时，CS可以以很高的概率完美恢复$x$。实践中，$x$的稀疏性要求可以被$x$在某个基$\Phi$下的稀疏性所替代，如傅立叶基或小波基，这样$\Phi x$可以表示非稀疏信号如自然图像等。CS理论的核心是限制保距性（Restricted Isometry Property，RIP），其定义为

$\begin{aligned} (1-\delta) \lVert \boldsymbol x_1-\boldsymbol x_2\rVert_2^2 & \leq \lVert \mathbf F(\boldsymbol x_1-\boldsymbol x_2)\rVert_2^2 \\ & \leq (1+\delta)\lVert \boldsymbol x_1+\boldsymbol x_2\rVert_2^2 \end{aligned}$

这里$\delta\in(0,1)$，是一个小常数。RIP表明，从$\mathbf F$的投影将距离保留在了由$1-\delta$和$1+\delta$所约束的两个信号之间。对于各种随机矩阵$\mathbf F$和稀疏向量$\boldsymbol x$，这个性质有很高的概率保留。这个性质保证在$\boldsymbol x$稀疏的约束下将测量误差最小化，以很高的概率得到精确的重建$\hat{\boldsymbol x}\approx \boldsymbol x$。重建公式为

$\hat{\boldsymbol x} = \argmin_{\boldsymbol x} \lVert \boldsymbol m-\mathbf F\boldsymbol x \rVert_2^2$

这个约束优化问题很难计算，但采样过程相对简单。

2.3.2 Compressed Sensing using Generative Models

稀疏性的要求限制了CS的应用，傅立叶基和小波基也只是部分缓解了这种限制，因为它们只能用于已知在这些基中稀疏的域。Bora et al., 2017提出使用生成模型的压缩感知（Compressed Sensing using Generative Models, CSGM）放宽这种要求。这个模型使用VAE或GAN预训练的深度神经网络$G_\theta$作为稀疏性的结构约束。这个生成器将一个潜在表示$\boldsymbol z$映射到信号空间：$\boldsymbol x = G_\theta(\boldsymbol z)$。$G_\theta$ 不要求稀疏信号，而是利用其架构和适应数据的权重将输出$\boldsymbol x$隐式地约束在低维流形内。这种约束足以为随机矩阵提供广义的集限制特征值条件（Set-Restricted Eigenvalue Condition，S-REC），可以以较高的概率实现较低的重建误差。重建使用一个类似于CS的最小化过程：

$\begin{aligned} \hat{\boldsymbol z} &= \argmin_{\boldsymbol z} E_\theta(\boldsymbol m,\boldsymbol z) \\ &= \argmin_{\boldsymbol z}\lVert \boldsymbol m - \mathbf FG_\theta(\boldsymbol z)\rVert_2^2 \end{aligned}$

重建信号为$\hat{\boldsymbol x} = G_\theta(\boldsymbol z)$。上式$\argmin$难以优化，可从随机采样点$\hat{\boldsymbol z} = p_{\boldsymbol z}(\boldsymbol z)$处开始进行梯度下降

$\hat{\boldsymbol z} = \hat{\boldsymbol z} - \alpha\frac{\partial E_\theta(\boldsymbol m,\boldsymbol z)}{\partial \boldsymbol z}\bigg\lvert_{\boldsymbol z=\hat{\boldsymbol z}}$

通常，需要数百或数千个梯度下降步骤以及从初始步骤重新启动几个步骤才能获得足够好的$\hat{z}$。Bora et al., 2017; Bojanowski et al., 2018。这项工作建立了压缩感知与深度神经网络的联系，且优于LassoTibshirani, 1996。Hand & Voroninski, 2017; , Dhar et al., 2018有在理论与实践上的进展。但仍有两方面的限制：

1. 重建的优化需要上千步梯度下降，依然很慢
2. 依赖于随机测量矩阵，对自然图像这样的高度结构化数据并不是最优的，经过学习的测量可能表现更好

2.3.3 Model-Agnostic Meta-Learning

元学习允许模型通过自我完善来适应新任务，与模型无关的元学习（MAML）提供了一种通用的方法来为许多任务调整参数Finn et al., 2017。

文章提出的MAML可以用于任何使用梯度下降进行训练的问题和模型，除了深度神经网络，分类、回归、策略梯度强化学习等不同的结构和任务都可以在很小的改动下解决。在元学习中，训练模型的目标是从新的小规模样本中快速学习新任务，此外，模型由元学习器训练以有能力学习大量的不同任务。关键思路是训练模型的初始化参数，以使模型在新任务上通过计算少量新的数据进行一次或多次梯度步骤更新参数而拥有最好的性能。不像之前的思路，更新函数或学习规则，这个算法没有增加学习参数的数量，也不对模型做限制。

对每个任务：

$\theta_i' = \theta - \alpha \nabla_\theta \mathcal{L_{T_i}}(f_\theta)$

元学习：

$\theta \leftarrow \theta - \beta \nabla_\theta \sum_{\mathcal{T}\sim p(\mathcal{T})} \mathcal{L_{T_i}}(f_{\theta_i'})$

2.3.4 Generative Adversarial Networks

生成对抗网络（GAN）训练参数化生成器$G_\theta$欺骗鉴别器$D_\varphi$，该鉴别器试图将真实数据与从生成器采样的虚假数据区分开来Goodfellow et al., 2014。

$\min_G \max_D V(D,G) = \mathbb{E}_{x \sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{x \sim p_{data}(x)}[\log(1- D(G(z))]$

2.3 深度压缩感知

首先，把 MAML 与 CSGM 相结合；之后将测量矩阵参数化，如使用 DNN。之前的工作使用随机映射作为测量，本文则将 RIP 作为训练目标，学习测量函数。之后通过在测量中施加 RIP 以外的其他性质，产生了两个新模型，包括带有判别器引导的潜在优化的 GAN 模型，导致更稳定的训练动态和更好的结果。

2.3.1 元学习压缩感知

CSGM 使用梯度下降，在隐空间内优化损失函数：

$\argmin_{\boldsymbol z}\lVert \boldsymbol m - \mathbf FG_\theta(\boldsymbol z)\rVert_2^2$

然而，这种优化可能需要上千个优化步骤，效率比较低。本文提出使用元学习的方法来优化这个重建过程。

3. Compressed Sensing using Generative Models

3.1 Abstract

The goal of compressed sensing is to estimate a vector from an underdetermined system of noisy linear measurements, by making use of prior knowledge on the structure of vectors in the relevant domain. For almost all results in this literature, the structure is represented by sparsity in a well-chosen basis. We show how to achieve guarantees similar to standard compressed sensing but without employing sparsity at all. Instead, we suppose that vectors lie near the range of a generative model $G : \mathbb{R}^k \Rightarrow \mathbb{R}^n$. Our main theorem is that, if G is L-Lipschitz, then roughly $\mathcal{O}(k \log L)$ random Gaussian measurements suffice for an $l_1/l_2$ recovery guarantee. We demonstrate our results using generative models from published variational autoencoder and generative adversarial networks. Our method can use 5-10x fewer measurements than Lasso for the same accuracy.

压缩感知的目标是通过利用相关域内向量结构的先验知识，从欠定的噪声线性测量系统中估计向量。在几乎所有相关文献的结果里，结构由在精心选择的基中的稀疏性所表示。我们展示了如何在完全不使用稀疏性的情况下实现与标准压缩感知相似的保证。与之相反，我们假设向量位于生成模型$G : \mathbb{R}^k \Rightarrow \mathbb{R}^n$的范围附近。我们主要的定理是，如果G是L-Lipschitz，那大约$\mathcal{O}(k \log L)$的随机高斯测量足以满足$l_1/l_2$的恢复保证。我们使用已发布的变分自动编码器和生成对抗网络的生成模型展示了我们的结果。我们的方法在相同精度下比Lasso使用少5到10倍的测量。

3.2 Introduction

$y = Ax^* + \eta$

其中，$A\in \mathbb{R}^{m\times n}, x^*\in \mathbb{R}^n, \eta \in \mathbb{R}^m$。这是一个欠定问题，求其最稀疏的解是一个NP难问题。如果A满足RIP或REC等条件，可以将其转化为凸优化问题，得到x的恢复。这方面有很多应用被研究，如计算断层扫描仪（CT），快速MRI等，以及单像素相机。

这篇文章依赖于生成模型产生的结构，而不是稀疏性。VAE、GAN等基于神经网络的生成模型在对数据分布建模上取得很多成果。这些模型的生成部件学习一个从低维表示空间$z\in\mathbb{R}^k$到高维样本空间$G(z)\in \mathbb{R}^n$的映射。训练时，这个映射被鼓励产生与训练集相似的向量，因此可以使用预训练的生成器大致获取我们的域中“自然”向量的概念，因为生成器定义了样本空间向量上的一个分布。

主要创新：提出了一个使用生成模型进行压缩感知的算法。使用梯度下降优化表示$z\in \mathbb{R}^k$，使得对应的图像$G(z)$有更小的测量误差$\lVert AG(z) - y\rVert_2^2$。这个目标函数非凸，但我们发现梯度下降效果很好，结果在很少的测量下优于Lasso。

我们的理论结果表明，只要梯度下降可以找到我们目标的良好近似解，输出$G(z)$就可以几乎与真实的$x^*$一样。

有定理：如果测量矩阵在给定生成器G的范围内满足S-REC，那么最小化测量误差的最佳值接近真实的$x^*$。进一步地，随机高斯测量矩阵很大概率满足大部分的生成器的S-REC条件。

<!-- TODO -->

4. Task-Aware Compressed Sensing with Generative Adversarial Nets

4.1 Abstract

In recent years, neural network approaches have been widely adopted for machine learning tasks, with applications in computer vision. More recently, unsupervised generative models based on neural networks have been successfully applied to model data distributions via low-dimensional latent spaces. In this paper, we use Generative Adversarial Networks (GANs) to impose structure in compressed sensing problems, replacing the usual sparsity constraint. We propose to train the GANs in a task-aware fashion, specifically for reconstruction tasks. We also show that it is possible to train our model without using any (or much) non-compressed data. Finally, we show that the latent space of the GAN carries discriminative information and can further be regularized to generate input features for general inference tasks. We demonstrate the effectiveness of our method on a variety of reconstruction and classification problems.

近年来，神经网络方法已广泛用于机器学习任务，并应用于计算机视觉。最近，基于神经网络的无监督生成模型已成功应用于通过低维潜在空间进行数据分布建模。在本文中，我们使用生成对抗网络（GAN）在压缩感知问题中施加结构，从而取代了通常的稀疏约束。我们提出以任务感知方式训练GAN，尤其是针对重建任务。我们还表明，无需使用任何（或大量）非压缩数据即可训练模型。最后，我们证明了GAN的潜在空间带有判别信息，并且可以进一步进行正则化以生成用于一般推理任务的输入特征。我们证明了我们的方法在各种重构和分类问题上的有效性。

4.2 Introduction

这篇文章是在 [Bora et al.][1] 的基础上进行的工作。[Bora et al.] 使用生成模型替代了压缩感知问题中的稀疏性假设，并且证明在生成模型满足一定条件，且测量矩阵为独立同分布的随机高斯分布时，在很高的概率下有

$\lVert G(\hat{z}) - x \rVert_2 \leq 6\min_z \lVert G(z) - x \rVert_2 + 3\lVert \zeta \rVert_2 + 2 \epsilon \tag{1}$

[Bora et al.] 的文章中，损失函数取为

$loss(z) = \lVert y - AG(z) \rVert_2^2 + \lambda_{prior} \lVert z\rVert_2^2 \tag{2}$

[Kabkab et al.] 首先证明了，在一定的假设下，有

$\lim_{t\to \infty} \mathbb{E}_x \big[ \min_z\lVert G_t(z) - x \rVert_2 \big] = 0 \tag{3}$

这表明 (1) 式右侧非常小。但以上定理的假设太严格，很难达到，因此 [Kabkab et al.] 考虑进行任务感知的 GAN 训练，允许生成器 G 对压缩感知重建任务进行优化。[Kabkab et al.] 对 Goodfellow 提出的的 GAN 的训练过程进行了修改，增加了对 (2) 式损失函数进行 GD 优化的步骤，再利用得到的隐变量 $z$ 继续 D 与 G 的优化。通过这种方式将压缩感知引入到 GAN 的训练中，使用压缩感知指导 GAN 的隐变量的筛选，从而得到更好的 GAN。

更进一步地，考虑到在压缩感知的任务中对采样过程进行压缩，非压缩的数据往往难以获得，因此提出基于一小部分的非压缩数据及大部分的压缩数据作为训练集进行训练。此算法训练两个判别器和一个生成器，第一个判别器分辨实际的训练数据 $x$ 与生成数据 $G(z)$，第二个判别器分辨实际的压缩训练数据 $y$ 与生成数据 $AG(z)$。这种对原始GAN的训练算法的变化并不会影响生成器的表示能力。

因为隐变量 $z$ 比非压缩数据 $x$ 与压缩数据 $y$ 的维度更低，作者认为可以将 $z$ 作为特征应用到分类任务中，并为这类任务引入了对比损失函数 (Contrastive Loss)。

作者在 MNIST、F-MNIST、CelebA 三个数据集上进行了实验。

5. Compressed Sensing with Invertible Generative Models and Dependent Noise

5.1 Abstract

We study image inverse problems with invertible generative priors, specifically normalizing flow models. Our formulation views the solution as the Maximum a Posteriori (MAP) estimate of the image given the measurements. Our general formulation allows for non-linear differentiable forward operators and noise distributions with long-range dependencies. We establish theoretical recovery guarantees for denoising and compressed sensing under our framework. We also empirically validate our method on various inverse problems including compressed sensing with quantized measurements and denoising with dependent noise patterns.

我们研究具有可逆生成先验的图像逆问题，特别是归一化流量模型。我们的公式将解决方案视为给定测量值的图像的最大后验（MAP）估计值。 我们的一般公式允许非线性可微正向算子和具有长期依赖性的噪声分布。我们在我们的框架下为消噪和压缩感知建立了理论上的恢复保证。我们还根据经验验证了我们的方法在各种反问题上的应用，包括采用量化测量值进行压缩感测以及采用相关噪声模式进行降噪的方法。

5.2 Introduction

• 逆问题：从观测中重建未知的信号，图像等
• 对通过不可逆的正向过程获得观测结果的情况感兴趣，这里有信息损失
  • 成像算法依赖先验知识对成像数据建模
  • $y = f(x) + \delta$，$y$是观察到的测量，$f$是确定且已知的正向算子，$\delta$是可能有着复杂结构的加性噪声
  • $f$ 建模了物理过程，如MRI、压缩感知、相位检索
• 线性逆问题：$y=Ax+\delta$，测量矩阵为$A$；
  • 降噪，压缩感知，超分辨，图像补全
  • 稀疏或者说结构稀疏是很有影响力的用于逆问题的结构先验
  • 最近，深度生成模型作为图像先验被引入，性能优于稀疏先验
• 可逆深度生成模型
  • 或者说，归一化流，是一类新的深度生成模型，可以通过构造进行高效采样、反演、似然估计，deepmind Normalizing Flows for Probabilistic Modeling and Inference
  • Asim 的 Invertible generative models for inverse problems 与 Bora 的 csgm 相比，带来了显著的性能提升，尤其对于分布外的样本进行成像时。受此启发，我们扩展了 Asim 的思路到噪声分布与可微分的正向算子上
• 贡献如下：
  • 我们提出了一种通用公式，以获得相关噪声和一般正向算子的最大先验（MAP）估计重构；线性逆问题与高斯噪声使用 Asim 的思路
  • 将可逆生成模型应用到重建图像与结构噪声中；如处理可变方差的噪声或具有MNIST数字结构的从属噪声
  • 展现了重建方法的两种理论结果。降噪问题：如果生成模型的 log 似然函数在真实图像周围局部强凹，那么可以证明梯度下降实现了取决于局部凸度参数的误差的减小；压缩感知：随机测量矩阵，MAP公式下可以限制恢复误差
  • 实验显示了在具有各种复杂和相关结构噪声存在时完美的重建；使用此方法在 CelebA-HQ 和 MNIST 上进行了多种逆问题，包括降噪与量化的压缩感知

5.3 预备知识

5.3.1 可逆生成模型

• 可逆生成模型，AKA 归一化流模型，通过可微可逆的函数 $G$ 映射简单噪声来近似复杂分布，通常为独立高斯噪声
• 采样：简单分布生成 $z$，计算$x = G(z)$。
  • 因为 $G$ 是可逆的，由密度函数变换可知：$p(x) = p(z) \lvert det J_{G^{-1}}(x)\rvert$，即$\log p(x) = \log p(z) + \log\lvert det J_{G^{-1}}(x)\rvert$，其中 $det J_{G^{-1}}(x)$ 是$G^{-1}$在 $x$ 处的雅各布矩阵。
  • $\log p(z)$ 是简单分布，只要能快速计算 $G^{-1}$ 和对数行列式，在任意点 $x$ 处计算似然性就会很直接
  • 满足可计算的可逆与对数行列式的神经网络生成器：NICE、RealNVP、IAF、iResNet、Glow、FFJORD
• Normalizing Flows:
  • 归一化流通过应用一系列可逆转换函数将简单分布转换为复杂分布；根据变量变化的理论获得最终的分布
  • $\log p_i(z_i) = \log p_{i-1}(z_{i-1}) - \log \lvert\det \frac{df_i}{dz_{i-1}}\rvert$
  • $x = z_k = f_k \circ f_{k-1} \circ \cdots \circ f_1(z_0)$，所以
  • $\log p(x) = \log \pi_k(z_k) = \log \pi_0(z_0) - \sum_{i=1}^k \log |\det \frac{df_i}{dz_{i-1}}|$
  • 全链叫做归一化流；因此需满足1易计算反函数2雅各比行列式易计算这两个条件
• 归一化流模型
  • 训练目标：负对数似然：$\mathcal{L}(\mathcal{D}) = -\frac{1}{|\mathcal{D}|}\sum_{x\in\mathcal{D}}\log p(x)$
  • RealNVP：
    • Real-valued Non-Volume Preserving，堆叠一系列可逆双射变换函数。
    • 所谓双射函数，即仿射耦合层
      • 输入维度分解为两部分：1. 前d维保持 2. d+1到 D维，仿射变换（放缩平移），且放缩与平移的参数为前d维的函数
      • $y_{1:d} = x_{1:d}$；$y_{d+1:D} = x_{d+1:D} \odot\exp(s(x_{1:d})) + t(x_{1:d})$
    • 这种变换满足前述条件
      • $x_{1:d} = y_{1:d}$；$x_{d+1:D} = (y_{d+1:D} - t(y_{1:d})) \odot\exp(-s(y_{1:d}))$
      • $J = \begin{pmatrix} I_d & 0_{d*(D-d)} \\ \frac{\partial y_{d+1:D}}{\partial x_{1:d}} & diag(\exp(s(x_{1:d})))\end{pmatrix}$
    • 同时，不需要计算s和t的逆与雅各比，s和t可以很复杂，如使用神经网络
    • 每层保持不同的地方不变；BN有助于训练
    • 多尺度架构
  • NICE，Non-Linear Independent Component Estimation，非线性独立分量估计
    • RealNVP，取消放缩，只有平移
  • Glow：扩展RealNVP，1x1卷积替换反向排列。三个步骤：
    • Activation normalization 激活归一化：类似于BN的仿射变换，batchsize为1，参数可学习
    • 可逆1x1卷积：RealNVP各层间通道反向排列；输入输出数相同的1x1卷积是对通道排列的泛化。$f=conv2d(h;W)$，$h$维度$h*w*c$，$W$维度$c*c$。
      • $\log |\det \frac{\partial conv2d(h;W)}{\partial h}| = \log |\det W|^{h\cdot w} = h\cdot w\cdot \log |\det W|$
      • 逆 1x1卷积依赖于 $W^{-1}$，运算量很小
    • 仿射耦合层ACL：RealNVP

5.3.2 相关工作

• 深度生成先验用于压缩感知与其他逆问题始于Bora的CSGM，该文中GAN与VAE对压缩感知而言是一种有效的先验；
• 其他工作调研了两者结合的其他方法：
  • Dhar 在生成器的范围内添加了稀疏偏差
  • Van Veen 将未训练的CNN作为成像任务的先验，基于深度图像先验
  • Wu 的 DCS 使用元学习提升重建速度
  • Ardizzone 通过使用流模型对正向过程进行建模，可以通过模型的可逆性隐式学习逆过程
  • Asim 提出使用归一化流模型替换CSGM的GAN先验，报告了出色的泛化性能，尤其是在重构失配图像时

5.4 方法

MAP 公式

• 观测：$y = f(x) + \delta$，$x\sim p$，$\delta\sim p_{\Delta}$，$f$为确定可微正向算子
• 给定观测 $y$，最小化如下 loss 来恢复 $x$：
  • $L_{MAP}(x;y) \triangleq -\log p_{\Delta}(y-f(x)) - \log p(x)$
  • 这个loss的最小值是后验概率$p(x|y)$的最大后验(MAP)估计
• 定义可逆映射 $G$，使用流模型 $p_{G}(x)$ 对 $p(x)$ 建模。
  • 如果 $p_G(x)$比较完美，那么 $L_{MAP}(x;y) \triangleq -\log p_{\Delta}(y-f(x)) - \log p_G(x)$
  • 又 $z\sim \mathcal{N}(0,I_d),\,x=G(z)$，故 $L_G(z;y)\triangleq -\log p_{\Delta}(y-f(G(z))) - \log p_G(G(z))$
  • $\argmin_z L_G(z;y) = \argmin_x L_G(x;y)$
• 上述优化目标非凸，但可微，可以使用基于梯度的优化器；实践中，非完美模型与大致优化即可在很多任务上表现良好

与之前工作的联系

• 此文基于 Bora 的 CSGM 与 Asim 的 IGMIP
• CSGM：GAN Prior
  • $L_{Bora}(z;y) = \lVert y-f(G(z))\rVert^2 + \lambda \lVert z\rVert^2$
  • 通过隐变量的二范数正则化，将 $y$ 投影到生成器的值域上；与MAP loss不同
    • 生成器不可逆，将噪声映射到高维向量；真实图像可能不在生成器的值域内；Asim也指出了无法表示任意输入的问题，这确实导致重建效果不佳
    • 此公式无概率上的解释，因为 GAN 不提供似然
• Flow Prior
  • 同时匹配观测、最大化似然：$L(z;y) = \lVert y-f(G(z))\rVert^2-\gamma \log p_G(x)$
  • 当噪声为各向同性高斯分布时，即 $\delta\sim \mathcal{N}(0, \gamma I_d)$，MAP loss 即为这种形式。因为 $\log p_\Delta (\delta) = -\frac{1}{2\gamma} \lVert\delta\rVert^2-C$，因此
  • $\begin{aligned} \argmin_z L_G(z;y) &= \argmin_z -\log p_\Delta(y-f(G(z)))-\log p_G(G(z))\\ &=\argmin_z\frac{1}{2\gamma}\lVert y-f(G(z))\rVert^2 - \log p_G(G(z))\\ &=\argmin_z\lVert y-f(G(z))\rVert^2 - \gamma \log p_G(G(z))\end{aligned}$
  • 因为存在优化上的困难，Asim 提出代理loss $L_{Asim}(z;y) = \lVert y - f(G(z))\rVert^2 + \gamma \lVert z\rVert$
    • 假设噪声各向同性高斯，且流量先验保持保持体积不变，即对数行列式为常量，那么 $\log p_G(x) = \log p(z) + \log \lvert\det J_{G^{-1}}(x)\rvert = -\lVert z\rVert^2+C$
    • 那么 $\argmin_z L_G(z;y) = \lVert y - f(G(z))\rVert^2 + \gamma \lVert z\rVert^2$
    • 体积不变性的结构有 NICE 与带加性耦合层的Glow

5.5 理论分析

不考虑信号的特定结构如稀疏与低维高斯生成先验。考虑普通设定，研究预训练流模型如何降低去噪问题的误差或减少压缩感知问题的测量数。

去噪问题的理论保证

• $y = x^* + \delta$，$\delta\sim p_\Delta = \mathcal{N}(0, \sigma^2 I)$
• loss 为 $L(x) = q(x) + \frac{1}{2\sigma^2}\lVert x-y\rVert^2$，$q(x) = -\log p(x)$
• 定理：假设 $x^*$ 为模型 $p(x)$ 的局部最优点，假设 $x^*$的邻域球 $B^d_r(x^*) = \{x\in \mathbb{R}^d: \lVert x-x^*\rVert<r\}$ 上 $q(x)$ 满足强凸性，即 $H_q(x) \succeq \mu I$，可以证明梯度下降收敛值 $\bar{x}$ 满足 $\lVert \bar{x} = x^*\rVert \leq \frac{1}{\mu\sigma^2+1}\lVert\delta\rVert < \lVert\delta\rVert$
• 也就是说，局部强凸性提升了去噪的质量，$\mu$更大的定义良好的模型去噪更好；最大似然训练目标与更好的降噪性能保持一致。

压缩感知的理论保证

• $y = Ax^*+\delta$
• 定理：给定 $x^*$，$q=\log p(x^*)$，$S(q) = \{x|\log p(x) \geq q\}$ 是概率密度高于真实图像的集合，$A\in \mathbb{R}^{m\times d}$，服从 $\mathcal{N}(0,1/m)$，$\epsilon = \lVert \delta\rVert_2$。求解如下带约束优化问题：
• $\bar{x} \leftarrow \argmin_{x\in\mathbb{R}^{d},\lVert Ax-y\rVert_2 \leq \epsilon} \{-\log p(x)\}$
• 可得:
• $\mathbb{E}\lVert\bar{x} - x^*\rVert_2 \leq \sqrt{8\pi}(\frac{\omega(S(q))}{\sqrt{m}}+\epsilon)$
• 其中$\omega(K)$为集合 $K$ 的高斯平均宽度。高斯平均宽度与集合的大小同阶，而$q$越大，$S(q)$就越小，因此上述上界对高概率密度的$x^*$更紧。$x^*$是全局最大值时，复原误差为0。
  • 定义高斯平均宽度：$\omega(K) \triangleq \mathbb{E}_{g\sim \mathcal{N}(0,I_d)}[\sup_{x\in M(K)} |\langle g,x\rangle|]$，直觉上就是集合的复杂度。

5.6 实验

（1）非线性正向算子，（2）具有相关性的复杂噪声，以及（3）高维可伸缩性。

数据集与结构

• 多尺度 RealNVP 模型；MNIST 与 CelebA-HQ。
• 公开的预训练 Glow 模型
• 测试：100 for CelebA and 1000 for MNIST

基线方法

• Bora，Asim
• BM3D for denoising
• 1-bit compressed sensing，no LASSO as quantization and non-Gaussian noise

模型平滑参数

• $L_G(z;y)$ 中，未知的真实数据分布$p(x)$由流模型$p_G(x)$给出密度近似。因此对 $x$ 的复原依赖于密度估计的质量
• 基于似然的模型存在反直觉的性质：对分布外样本指定高密度
• 为纠正这一点，使用$p_G(x)^\beta$进行平滑
• $L_G(z;y;\beta) = -\log p_\Delta(y-f(G(z))) - \beta\log p_G(G(z))$
• $\beta=0$，only noise；$\beta=\infty$，only model；$\beta$ 控制对 $p_G$ 的依赖程度

结果

• 移除 MNIST 噪声：
  • $y = 0.5x+\delta_{MNIST}$，
  • 使用MNIST训练的流模型生成作为噪声，添加到不同的通道与位置上；
  • 图像分解任务
  • Bora 移除了，因为所有生成由DCGAN得到
• 移除正弦噪声：
  • $y = x + \delta_{sine}$，
  • 每行服从高斯分布，方差为正弦；
• 移除径向噪声：
  • $y = x + \delta_{radial}$，
  • 每个像素服从高斯分布，方差由中心向四周指数衰减
  • $\sigma(d) = \exp (-0.005d^2)$
• 带噪声的1比特压缩感知
  • 非线性正向算子与非高斯噪声
  • $y = sign(Ax) + \delta_{sine}$，$A\in\mathbb{R}^{m\times d}$为随机高斯测量矩阵，噪声为1维正弦噪声，具有恒定的偏移量，平均值为正
  • 最极端的量化压缩感知，观测结果为 $\{+1,-1\}^m$；正均值噪声使信号由负翻转为正，对零均值假设进行了挑战
  • 梯度为0，使用 straight-through estimator 进行反向传播
• 亚像素插补
  • $y = M \odot x$，$M$ 为随机二值mask；随机丢掉 25%的亚像素，尝试补全
  • 线性无噪声，256*256 图片，预训练Glow模型
  • 结果证实方法与框架无关，恢复质量与运行时间可扩展到高维

5.7 结论

• 提出新方法，逆问题，通用可微正向算子，结构噪声
• 与基线的比较不公平，因为此方法了解噪声结构，其他方法没有这种设计
• 可视为 Asim 的补充到更通用的正向算子与噪声模型
• 我们的方法之所以强大，是因为可逆生成模型的灵活性，可以将其以模块化的方式组合起来，以解决非常普遍的情况下的MAP逆问题。
• 仍然存在的中心理论问题是分析我们制定的优化问题。
• 在本文中，我们使用梯度下降从经验上最小化了这种损失，但一些理论上的保证可能会非常有趣，可能是在假设条件下，例如： 随机权重遵循Hand和Voroninski的框架

6. Back-Projection based Fidelity Term for Ill-Posed Inverse Problems

不适定线性逆问题的基于反投影的保真项

6.1 Introduction

Ill-posed linear inverse problems appear in many image processing applications, such as deblurring, super- resolution and compressed sensing. Many restoration strategies involve minimizing a cost function, which is composed of fidelity and prior terms, balanced by a regularization parameter. While a vast amount of research has been focused on different prior models, the fidelity term is almost always chosen to be the least squares (LS) objective, that encourages fitting the linearly transformed optimization variable to the observations. In this paper, we examine a different fidelity term, which has been implicitly used by the recently proposed iterative denoising and backward projections (IDBP) framework. This term encourages agreement between the projection of the optimization variable onto the row space of the linear operator and the pseudo- inverse of the linear operator (“back-projection”) applied on the observations. We analytically examine the difference between the two fidelity terms for Tikhonov regularization and identify cases (such as a badly conditioned linear operator) where the new term has an advantage over the standard LS one. Moreover, we demonstrate empirically that the behavior of the two induced cost functions for sophisticated convex and non-convex priors, such as total-variation, BM3D, and deep generative models, correlates with the obtained theoretical analysis

不适定的线性逆问题出现在许多图像处理应用中，例如去模糊，超分辨率和压缩感知。许多恢复策略涉及使成本函数最小化，该成本函数由保真度和先验项组成，并由正则化参数进行平衡。大量研究集中在不同的先前模型上，但保真度术语几乎总是被选为最小二乘（LS）的目标，这鼓励将线性变换的优化变量拟合到观测值。在本文中，我们检查了一个不同的保真度项，该项已被最近提出的迭代去噪和反向投影（IDBP）框架隐式使用。该项鼓励优化变量在线性算子的行空间上的投影与应用于观测值的线性算子的伪逆（“反投影”）之间的一致。我们分析了两个保真项之间的差异，以进行Tikhonov正则化，并确定了新项比标准LS项具有优势的情况（例如条件不佳的线性算子）。此外，我们通过经验证明，复杂的凸和非凸先验的两个诱导成本函数的行为，例如总变异，BM3D和深度生成模型，与所得理论分析相关。

• $y=Ax+e,\,x\in\mathbb{R}^n$